Definición y ejercicios del Teorema de Tales
Si te estás preparando para presentar la Prueba de Acceso a la Educación Superior, conocer a fondo todos los temas, especialmente los de las pruebas obligatorias, será una de las herramientas que te ayudarán a alcanzar el mejor puntaje.
Por eso, en este blog te explicamos paso por paso el teorema de Thales, concepto fundamental para la prueba de matemática M1. Además, te dejamos algunos ejemplos y ejercicios que tiene una estructura y dificultad semejante a las de tu examen.
¿Qué es el teorema de Tales?
Tales de Mileto fue un filósofo de la antigua Grecia que se enfocó en estudiar la naturaleza y la geometría. Entre sus principales aportaciones está el teorema de Thales el cual es muy útil para encontrar la medida de los lados entre triángulos semejantes.
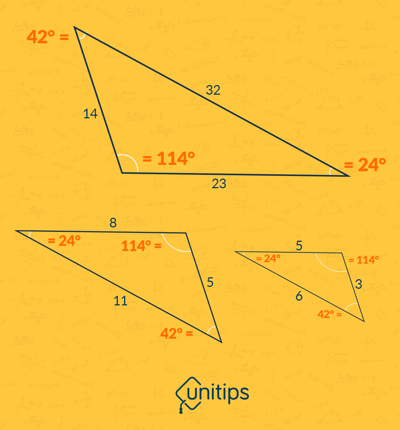
Los triángulos semejantes son aquellos cuyos ángulos internos tienen la misma medida. Por ejemplo, los siguientes triángulos tienen lados con medidas y disposiciones diferentes, pero con ángulos idénticos, por lo que son considerados semejantes.
También observó que, si se traza una línea paralela dentro de un triángulo a cualquiera de sus lados, se forman dos triángulos semejantes, por lo que Tales encontró que el cociente que se obtiene al relacionar los lados del triángulo original con los lados del triángulo nuevo es el mismo.
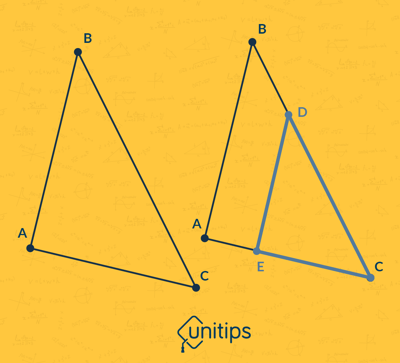
En palabras simplificadas, el teorema de Thales explica que, al trazar una línea paralela al lado de un triángulo, el triángulo obtenido será semejante al original. Esto se expresa con la siguiente fórmula:
$${BC/DC=AC/EC=AB/DE}$$
Además, esto quiere decir que, si elegimos un lado del triángulo original y lo dividimos en el correspondiente del triángulo semejante, obtendremos el mismo valor que si elegimos otro de los lados y se divide en su equivalente.
Si sientes que necesitas apoyo extra para estudiar este y otros temas de la prueba obligatoria de Matemáticas M1, entonces te sugerimos que des clic en el siguiente enlace y accedas a la versión gratuita del preuniversitario Unitips, donde a partir de clases animadas, miniquizzes y ensayos en línea, podrás prepararte para el ingreso a la universidad.
¿Para qué sirve el teorema de Thales?
Con el teorema de Thales estableceremos una ecuación con el cociente de los lados cuyas medidas conocemos y lo igualaremos con el cociente de los lados en donde aparezca el lado que queremos conocer.
Revisemos este ejemplo de acuerdo con los datos del ejemplo anterior:
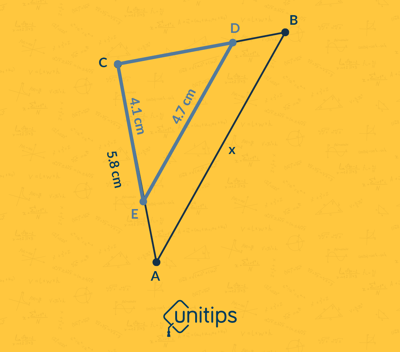
Conocemos la medida del lado CA correspondiente al triángulo exterior, el cual relacionaremos con el que le corresponde del triángulo interior que también conocemos, es decir CE. Esta expresión se iguala con el lado desconocido AB, dividido en el lado conocido DE. Se expresa de la siguiente forma:
$$\frac{CA}{CE}=\frac{AB}{DE}$$
Ahora sustituiremos las incógnitas con los valores que sí conocemos:
$$\frac{5,8\ cm}{4,1\ cm}=\frac{x}{4,7\ cm}$$
Esta ecuación se resuelve fácilmente despejando a la “x” multiplicando por 4,7 cm:
$$ x=\frac{5,8}{4,1}\times4,7=6,7$$
Por lo tanto, el lado AB mide 6,7 cm.
Ejemplos resueltos del teorema de Tales
Una aplicación importante de este teorema es calcular medidas de segmentos que se forman entre dos rectas cualquiera cortadas por rectas paralelas. Revisemos el siguiente ejemplo:
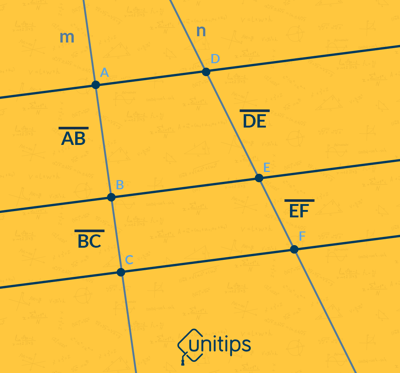
Debido a que se cumple la proporcionalidad entre los segmentos, el teorema de Thales indica que podemos relacionar a los cocientes de la siguiente manera:
$$\frac{\bar{AC}}{\bar{DF}}=\frac{\bar{AB}}{\bar{DE}}=\frac{\bar{BC}}{\bar{EF}}$$
Ahora, veamos el siguiente: las líneas mostradas en color negro son paralelas entre sí, pero ¿cuál es la medida del segmento “x”?
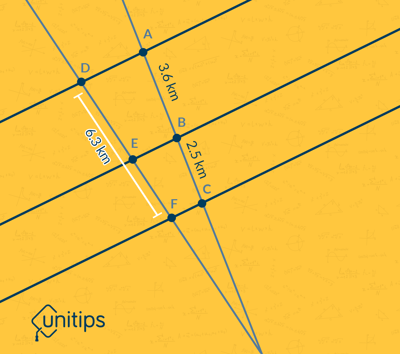
El segmento “x”, junto con “y”, son partes del segmento que mide 6,3 km. El teorema de Thales nos permite relacionar los cocientes de los lados opuestos de la siguiente manera:
$$\frac{x}{2,5\ km}=\frac{y}{3,6\ km}$$
Para poder resolver la ecuación anterior, escribiremos a “y” en términos de “x”, sabiendo que:
$$ x+y=6,3\ km$$
$$ y=6,3\ km\ -x$$
Al sustituir la expresión anterior en la relación original, podemos obtener una ecuación en términos de “x”:
$$\frac{x}{2,5\ km}=\frac{6,3\ km\ -x}{3,6\ km}$$
El proceso de solución sería el siguiente:
$$(3,6)(x)=(2,5)(6,3-x)$$
$$13,6x=15,75-2,5x$$
$$13,6x+2,5x=15,75$$
$$16,1x=15,75$$
$$\frac{15,75}{6,1}=2,6\ km$$
El segmento “x” mide 2,6 km, lo cual nos permite conocer también la medida del segmento “y” porque es la diferencia de 6,3 km y 2,6 km, es decir:
$$ y=6,3-2,6=3,7\ km$$
Una de las aplicaciones más utilizadas del teorema de Tales es la medición indirecta de alturas de estructuras de gran tamaño. Por ejemplo, para conocer la altura de la gran pirámide de Guiza en Egipto, es posible utilizar al largo de la sombra proyectada por la pirámide a cierta hora por la tarde y compararla con el largo de la sombra que cualquier objeto con altura conocida proyecte.
En este caso utilizaremos una palmera de 4 metros de alto. Si el largo de la sombra proyectada por la pirámide es de 300 metros y el de la palmera es de 8,6 metros, ¿cuál es la altura de la pirámide?
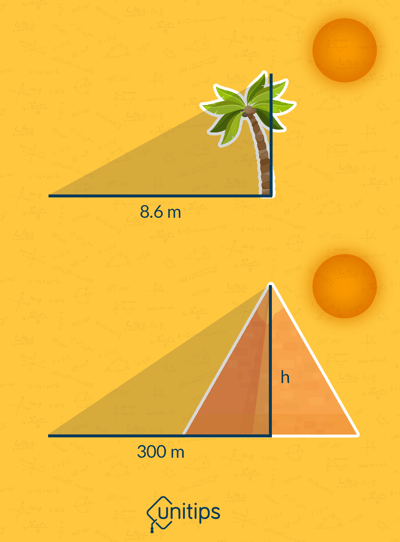
Para solucionar este problema, es necesario que observes los dos triángulos que forman la pirámide y la palmera con sus respectivas sombras a la misma hora del día. Se trata de triángulos semejantes, por lo que podemos establecer que:
$$\frac{altura\ de\ la\ piramide}{altura\ de\ la\ palmera}=\frac{sombra\ de\ la\ piramide}{sombra\ de\ la\ palmera}$$
$$\frac{h}{4\ m}=\frac{300\ m}{8,6\ m}$$
Al multiplicar por 4 al resultado de dividir 300 en 8,6 encontramos la altura de la pirámide:
$$h=\frac{300\ m}{8,6\ m}\times4$$
$$h=139,5\ m$$
Esperamos que estos ejemplos te hayan ayudado a repasar el tema del teorema de Tales y ahora te sientas con más seguridad para dar la PAES. Continúa preparándote con recursos en línea y mide tu nivel académico con un ensayo en línea, sólo necesitas registrarte en el siguiente enlace para acceder a uno.
Ejercicios de teorema de Tales
Ahora que tienes esta información, repasar con ejercicios extra te ayudará a mejorar tu desempeño en matemáticas. Aquí te dejamos tres modelos de preguntas para la PAES obligatoria M1.
Copia las preguntas en una hoja e intenta resolverlas por tu cuenta. Al final de este blog, encontrarás las respuestas correctas.
Ejercicio 1. ¿Cuál es la medida del segmento “y”?
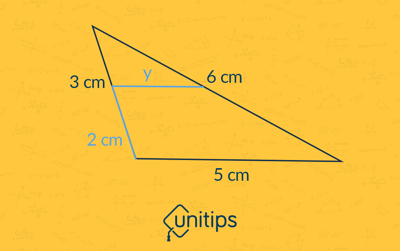
- 5 cm
- 2,5 cm
- 4 cm
- 3 cm
Ejercicio 2. Halla el valor de “x”.
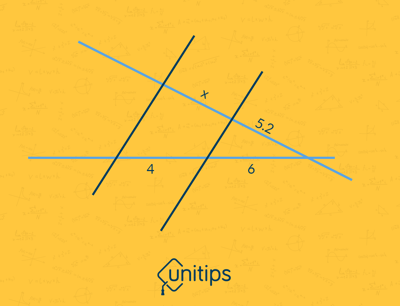
- 3,0
- 3,5
- 3,2
- 3,8
Ejercicio 3. ¿Cuál es la altura de una pared que proyecta una sombra de 15 metros de largo si al mismo tiempo un bastón de 30 cm clavado de forma perpendicular en el suelo proyecta una sombra de 20 cm?
- 200 m
- 25,5 m
- 22,5 m
- 20 m
Recuerda que, para lograr obtener un puntaje en tus PAES que te permita acceder a las universidades que quieres, necesitas prepararte adecuadamente y utilizar con recursos útiles y efectivos. Comienza a armar tu calendario de estudio y haz una planeación que se pueda ajustar a tus necesidades y tiempos.
En el preUnitips encontrarás clases animadas, miniquizzes, tutorías y ensayos ilimitados para preparar todas tus PAES desde una sola plataforma. Además, todos los recursos se encuentran disponibles 24/7, por lo que podrás adaptarte a tus intereses y estudios. Regístrate en el siguiente enlace y recibe una versión gratuita de tres lecciones.
Fuentes de consulta:
- Baldor, A. (2019). Geometría. Patria.
- Wheater, Carolyne C. (2019). Geometry Review and Workbook. McGraw Hill.
Respuestas:
- 3 cm
- 3,5 cm
- 22,5 m
