Función lineal y afín: tema de la PAES M1

Función lineal y afín: ejemplos y ejercicios

Conocer qué es la función lineal y afín es fundamental para entender temas subsecuentes de la asignatura de Matemáticas, así como para dar la PAES obligatoria M1 y así obtener un puntaje que te asegure un lugar en la universidad de tus sueños.

Para facilitar este proceso, en este blog te explicamos el concepto de estas funciones y revisaremos distintos ejemplos que te ayudarán a comprender mejor este tema.

¿Qué es una función?

Una función es toda relación matemática entre dos variables donde a cada valor de la variable independiente (dominio) le corresponde únicamente un valor de la variable dependiente (rango). Imaginemos que una función es como una máquina en la que se introduce un valor (“x”), se le aplica alguna operación conocida y arroja un resultado (“y”).

$$x\rightarrow\fbox{$f\left(x\right)$}\rightarrow\ y$$

La función usualmente la representamos con la letra “f” y las variables que serán modificadas las llamamos “x”, de manera que la función se expresa como:

$$ f\left(x\right)$$

Para entender mejor el concepto de las funciones, veamos un ejemplo: supongamos que tenemos una función encargada de triplicar todos los valores que se introduzcan. En este caso, la representaremos como una multiplicación por 3, o sea:

$$ f\left(x\right)=3x $$

$$ x\rightarrow\fbox{$3x$}\rightarrow\ y $$

La función es capaz de triplicar cualquier valor de “x”, como es imposible mostrarlos a todos, utilizaremos solo a algunos:

La columna izquierda indica el valor que se “introdujo” en la función y la de la derecha muestra el resultado que se obtiene al operarla.

En un plano coordenado es posible representar gráficamente la relación entre una función y las variables si a cada par de datos los representamos como coordenadas (x,y), siendo “y” el valor de la función. Veamos:

Ubicamos estos puntos en un plano y marcamos la recta que forman. En esta recta, en color rojo, se encuentran todas las parejas de datos de entrada y salida que puede haber en la función f(x)=3x.

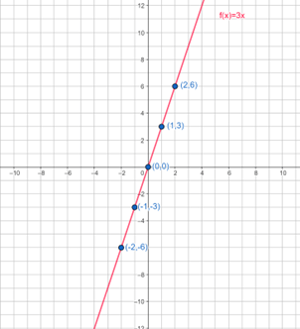
Observa que, si elegimos un valor de “x”, digamos x=4, la función lo triplicará y nos dará el número 12, el punto (4,12) forma parte de la recta.

Esto lo indicamos como:

$$ f\left(4\right)=3\times4=12$$

Si estás buscando otro tipo de recursos que te ayuden a estudiar la función lineal y afín, así como el resto de temas de las PAES que te tocan rendir, matricúlate sin costo en el preuniversitario Unitips en línea, donde podrás estudiar a través de clases animadas y breves, además de complementar con trivias breves y tutorías. Haz clic al siguiente examen y conócelo. ⬇💻

Pendiente “m”

Ahora bien, es importante conocer también el concepto de pendiente, que se refiere a la manera en la que medimos la razón de cambio, es decir, qué tanto crece o decrece la función cuando aumentan los valores de “x”. Observa el comportamiento de distintas funciones en la siguiente imagen:

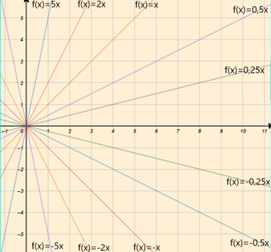
La inclinación que tiene una recta depende de su pendiente; entre más grande sea, más inclinada estará la recta, esto es porque la pendiente indica el número por el que se multiplica “x”. Entre más grande sea este, la función tendrá valores más grandes. También observa que, con valores negativos de pendiente, la función decrecerá, es decir, si los valores de “x” aumentan, se comportará de manera opuesta disminuyendo sus valores.

Función lineal

Ahora bien, las funciones lineales son aquellas expresiones del tipo y=mx, donde el valor de m es cualquiera menos 0. Se distingue también porque, al representarse en una gráfica, pasa por el origen, es decir, por los puntos (0, 0). Revisemos un ejemplo de la función lineal para que puedas comprenderla mejor.

Martina vende empanadas a sus amigos y el precio de cada una es $800. Encuentra una función que describa la cantidad de dinero que obtiene respecto al número de empanadas vendidas y grafícalo. ¿Cuánto dinero recibe si vende 3, 5 y 85 empanadas?

Sabemos que es una función lineal debido a que el dinero que obtiene al vender cada empanada es el mismo sin importar el número que venda. La variable “x” será la cantidad de empanadas vendidas y la función nos dirá la cantidad de dinero obtenido.

La pendiente de esta función es la razón de cambio, es decir, la cantidad de dinero que se obtiene con cada empanada vendida, en este caso la pendiente “m” es 800.

$$ f\left(x\right)=800x $$

En donde:

• f(x) es la cantidad de dinero por las ventas
• x es la cantidad de empanadas vendidas
• 800 es el precio de cada empanada, es decir, la cantidad que aumentará la cantidad obtenida con cada empanada vendida.

Para graficar utilizaremos una tabla para obtener las coordenadas de algunos puntos pertenecientes a esta función.

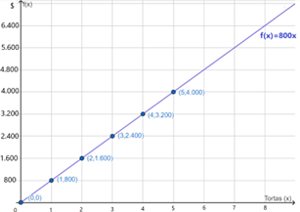
Utilizaremos a la función lineal para encontrar la cantidad de dinero que se obtiene al vender 3, 5 y 85 empanadas:

3 empanadas x=3

$$ f\left(3\right)=800\times3=2.400$$

5 empanadas x=5

$$ f\left(3\right)=800\times5=4.000$$

85 empanadas

$$ f\left(3\right)=800\times85=68.000$$

Practica este y otros temas de tu prueba PAES obligatoria de Matemáticas y resuelve el ensayo gratuito en línea que te obsequia el preUnitips. Para obtenerlo, sólo necesitas crear tu cuenta, iniciar sesión y dar clic en la pestaña “Ensayos”.

Función afín

Por otra parte, la función afín se expresa como y=mx+n, cuando m y n tienen valores distintos a 0. A diferencia de la lineal, esta función no pasa por el centro (0, 0). Veamos un ejemplo.

Veamos un ejemplo diferente para entender este tipo de funciones.

Un vendedor de seguros recibe un sueldo base mensual de $300.000, a este monto se le agrega una comisión de $20.000 por cada seguro de vida que consigue vender. Determina su sueldo si en un determinado mes:

1. No logra vender ningún seguro
2. Vende 2 seguros
3. Vende 6 seguros

Este caso muestra diferencias respecto a las funciones lineales porque su sueldo no depende únicamente de la cantidad de seguros que venda, sino que hay un monto fijo que ya tiene asegurado.

La función cambia porque es necesario agregar dicho monto inicial. Observa que la pendiente también es la razón de cambio, es decir, la cantidad que recibe por cada seguro que vende, por lo anterior, la función se puede expresar de la siguiente manera:

$$ f\left(x\right)=20.000x+300.000$$

En donde:

• f(x) es el sueldo total que recibe en un mes
• x es el número de seguros que logró vender
• 000 es el sueldo que tiene asegurado, a este valor se le llama coeficiente de posición.

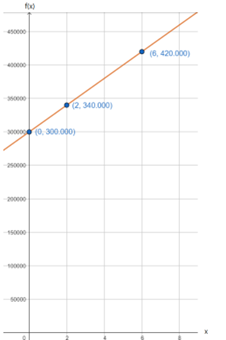
Realicemos la gráfica utilizando los casos de seguros vendidos que se nos piden.

Ubicamos los puntos en un plano cartesiano y los unimos:

Diferencias entre función lineal y afín

Ahora ya conoces las principales características de las funciones lineales y afines. Sin embargo, para que te quede más claro, te resumimos sus diferencias en el siguiente cuadro. Si se te complica estudiar matemáticas, usar estrategias como cuadros, mapas mentales y gráficas te funcionará.

Ejercicios de función lineal y afín

Como en las matemáticas lo más importante es poner en práctica tus conocimientos, a continuación, te compartimos tres ejercicios similares a los que te enfrentarías en la PAES M1. Responderlos te ayudará a saber qué tanta preparación tienes o si es necesario que estudies con recursos extra.

Ejercicio 1. La siguiente opción NO es una característica de la función f(x)=13x+1.

1. Cuando x=0, la función vale 0
2. La pendiente es 13
3. El coeficiente de posición es 1
4. Es una función afín

Ejercicio 2. ¿Cuál de los siguientes gráficos corresponde a la función f(x)=4x?

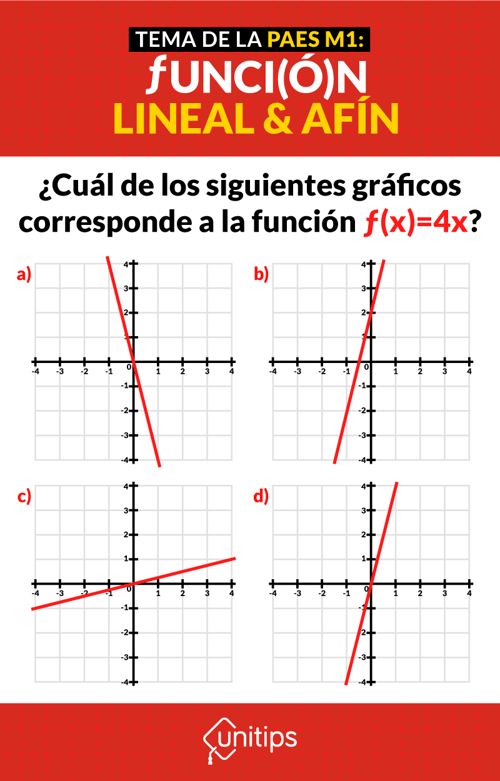
Ejercicio 3. El grifo de un baño tiene una fuga que deja salir 15 ml de agua cada minuto. Para evitar el desperdicio se utiliza un recipiente de gran capacidad que no se encuentra vacío dado que ya contiene 650 ml de agua.

¿Cuál de las siguientes opciones es una función válida para modelar la cantidad de agua que habrá en el recipiente después de x minutos?

1. f(x)= 650x
2. f(x)= 15x +650
3. f(x)= 650x + 15
4. f(x)= 15x

En la pregunta anterior, ¿Cuál es la cantidad de agua (en ml) que habrá en el recipiente después de 20 minutos?

1. 665
2. 750
3. 950
4. 300

¿Aún necesitas estudiar más temas de la PAES M1? Entonces revisa los siguientes blogs, donde te explicamos algunos conceptos fundamentales para esta prueba:

• Transformaciones isométricas
• Teorema de Tales

También puedes registrarte a la versión gratuita del preuniversitario Unitips. Con él podrás estudiar en una sola plataforma todos los contenidos de las PAES obligatorias y electivas, además de practicar con ensayos ilimitados y tutorías personalizadas. Haz clic en el siguiente enlace y conócelo gratis.

«Estudia 24/7 desde tu computadora o smartphone. Regístrate aquí y recibe tres clases más un ensayo gratuito.»

Respuestas:

1. a)
2. d)
3. b)
4. c)